1. Fonction de transfert. 

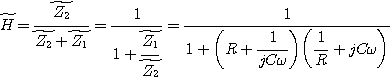
Soient Z1 l'impédance de la portion (R, C) série et Z2 celle de la portion (R, C) parallèle. Le circuit forme un pont diviseur de tension au niveau des deux associations précédentes. On a :

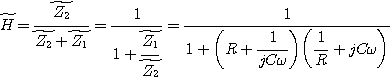
2. Courbe de réponse en gain. Bande passante.
Le gain exprimé en décibels a pour expression :

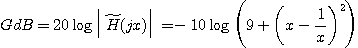
La courbe de réponse en gain admet :

• en basse fréquence : une asymptote passant par l'origine de pente + 20 dB/ décade

  GBF = 20 log x = 20 X

• en haute fréquence :
  une asymptote passant par l'origine de pente - 20 dB/décade

  GHF = -20 log x = - 20 X

Le diagramme asymptotique est la réunion des deux asymptotes haute et basse fréquence limitées à leur point de concours I.

La qualité de cette représentation s'évalue en calculant en x = 1 l'écart entre la représentation asymptotique et la réponse en gain :

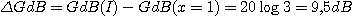
Cet écart n'est pas trop important.

Le filtre se comporte comme un passe-bande.

On détermine à présent sa bande passante.

Les limites de la bande passante sont données par l'équation :

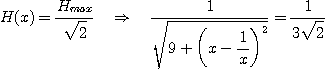
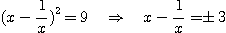
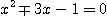
On ne conserve que les racines positives de ces deux équations :

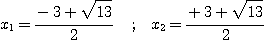
X1 = - 0,52   ;   X2 = +0,52

La largeur de la bande passante à pour expression :

3. Comportement de la phase.

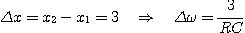
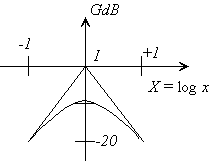
L'argument de la fonction de transfert est donné par :

La courbe de réponse en phase passe le point ( X  = 0,j= 0) et admet :

• en basse fréquence :
  une asymptote horizontale j= p/2.
• en haute fréquence :
  une asymptote horizontale j = - p/2.