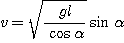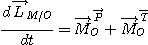
On travaille dans le référentiel terrestre supposé galiléen. On considère le point M de masse m. Les forces appliquées à ce système sont :
1. Application du théorème du moment cinétique.
Si le point M est animé d'un mouvement circulaire alors r et z sont des constantes.
On applique le théorème du moment cinétique au point M par rapport au point fixe O du référentiel galiléen d'étude.
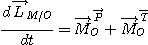
Le moment de la tension du fil par rapport à O est nul car les vecteurs T et OM sont colinéaires. D'autre part :
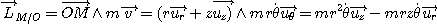
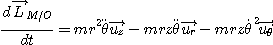
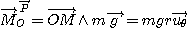
Par identification on obtient :
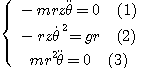
Les équations (1) et (3) montrent que le mouvement est uniforme car la vitesse angulaire est constante.
L'équation (2) permet d'écrire :
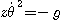
Or :
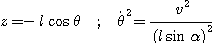
On obtient pour expression pour la vitesse à communiquer :
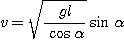
2. Application de la relation fondamentale de la dynamique.
On applique la relation fondamentale de la dynamique à la masse m :
mg + T = ma
Comme r et z sont des constantes, l'expression de l'accélération dans la base cylindro-polaire est :
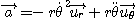
On projette la relation fondamentale dans la base cylindro-polaire liée au point M :
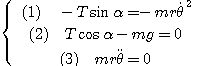
(3) montre que le mouvement de M est uniforme.
(2) permet d'exprimer la valeur de la tension en fonction de celle du poids l'on injecte dans (1) :
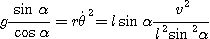
On obtient finalement :